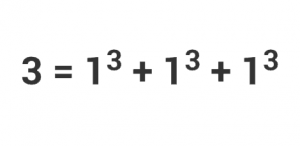Sums of Cubes Research Published
“On a question of Mordell” by Andrew Booker (Bristol) and collaboration PI Andrew Sutherland has been published in the Proceedings of the National Academy of Sciences. See MIT’s press release for how these solutions were found with the help of half a million home computers.