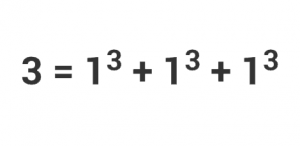
New Solution for the Sum of Three Cubes for 3!
It’s easy to represent 3 is a sum of three cubes 3 = 13 + 13 + 13, but can we characterize all the solutions of x3 + y3 + z3 = 3 with x, y, and z integers?
Until this week, the only other solution known was 43 + 43 + (-5)3 = 3.
Andrew Booker and collaboration PI Andrew Sutherland just found the next simplest solution
3 = 5699368212219623807203 + (-569936821113563493509)3 + (-472715493453327032)3
Read more about it:
- Bristol University press release: http://www.bristol.ac.uk/maths/news/2019/number-3.html
- AMS blog post: https://blogs.ams.org/beyondreviews/2019/09/18/3/#more-2526
- Quanta Magazine article: https://www.quantamagazine.org/why-the-sum-of-three-cubes-is-a-hard-math-problem-20191105/